The magic of the one-time pad

XOR, Perfect Secrecy, and the One-time Pad

Despite the amazing power of modern cryptography to protect our sensitive data, none of it is perfectly secure. With enough computing power and time, all modern encryption can be cracked. The unreasonably large time and spatial complexity make it reasonably secure (but not perfectly secure). We say it’s reasonable because, with our current technology, we’d reach the heat-death of the universe before you could brute-force attack a reasonably secure encryption key.

Yet, a perfectly secure, uncrackable technique has existed in one form or another for over 140 years — the one-time pad.

The one-time pad technique was originally discovered in 1882 by the cryptographer Frank Miller for use in telegraphy. But it wasn’t until an important invention in 1917 by Gilbert Vernam at Bell Labs, and that its adoption grew. Vernam invented an electromechanical device to perform the Exclusive or (XOR) operation on encoded messages.

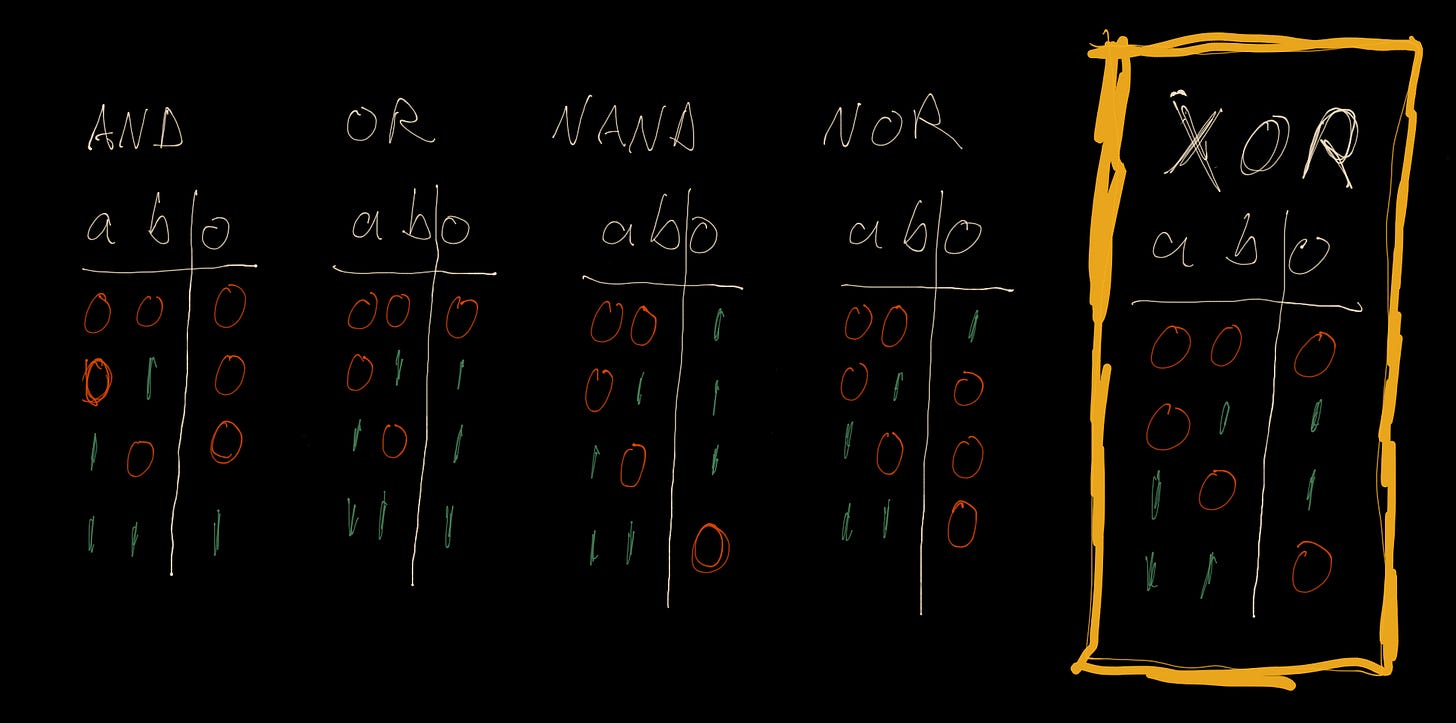
Below are pictured some common logic gates. If we look at the first row in AND, you can read it like “If a is 0 and b is 0, then the output is 0”. Look over these logic gates. What do you see that is unique about the XOR output?

The XOR is special in logic gates because it has a balanced output. This means that unlike the other logic gates, if you have a message encoded in 1s and 0s and a secret key made of 1s and 0s, the XOR gives us a 50/50 chance that your XOR output is either a one or a zero. The output of the XOR gate doesn’t tell you any information about what the values of a or b might have been.

Therefore, with an XOR gate, you can take any message and encrypt it by running it through an XOR with your secret key. One can decrypt the original message unless you have that original key. To decrypt the message, you simply XOR the encrypted message with the original key, and viola, you have your original message. The XOR doesn’t reveal any information when used to encrypt a message. Any input is equally likely to generate any output.

In his groundbreaking 1949 paper “Communication Theory of Secrecy Systems,” Claude Shannon established the unparalleled security of one-time pads. He proved that any cryptographic system aspiring to be perfectly secure must meet the same criteria as the one-time pad. This means that no amount of brute force attempts will ever reveal the encrypted message, instilling a sense of confidence in its effectiveness.

Of course, while this form of encryption is perfectly secure, it has flaws. It is impractical in day-to-day use. For instance, a secret key can never be reused. Reusing a key in a one-time pad makes you susceptible to statistical analysis attacks and breaks the security guarantee. It is also a symmetric algorithm, meaning two people interested in sharing messages must have pre-shared keys in person before you can communicate. Both parties would have to coordinate the order in which they use the keys, never reuse them, and if you ran out of keys in your one-time pad, you’d have to meet up again before you could share more messages.

I find it fascinating that, no matter how impractical the one-time pad is in day-to-day use, it is also the most resilient to attacks when used properly. There is a real risk that Quantum computers will break modern cryptography in a few years, but that isn’t true for our 140-year-old friend, the One-Time Pad. Quantum computers still can’t break perfect secrecy.