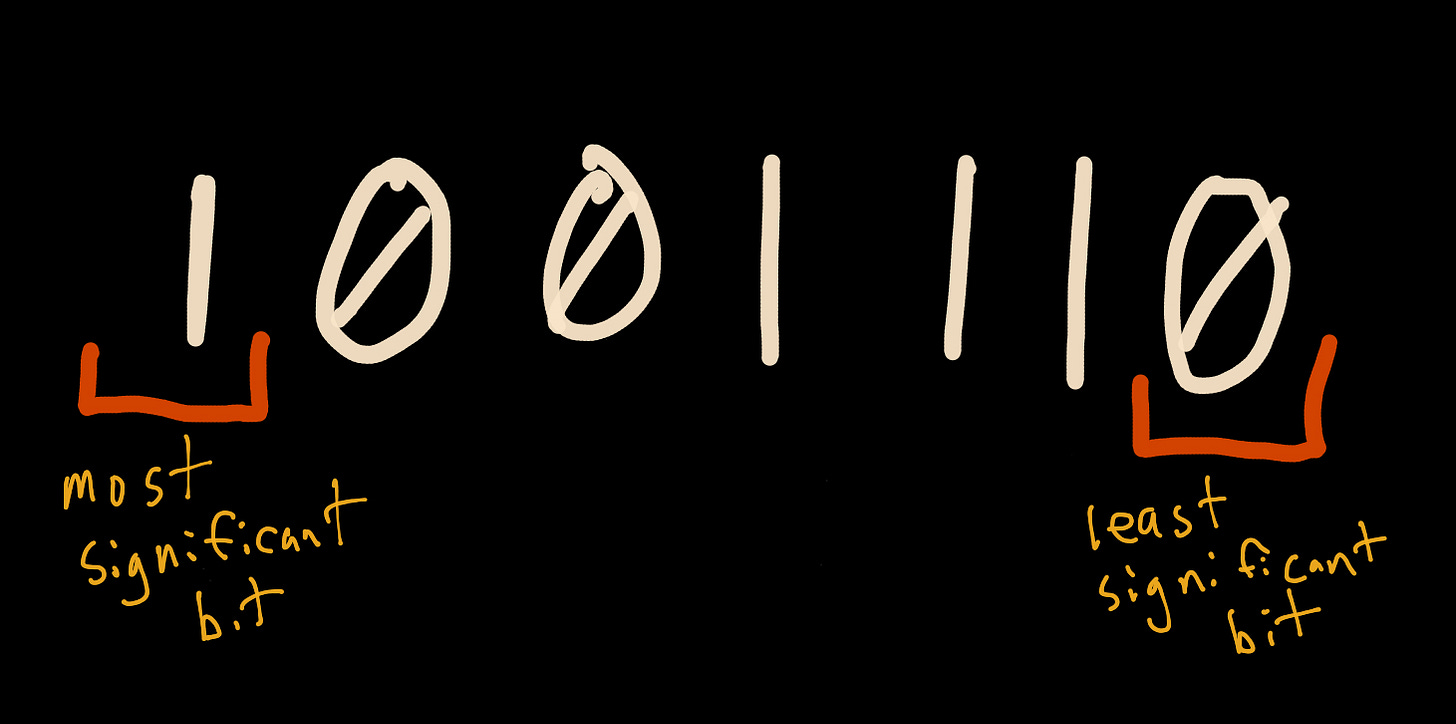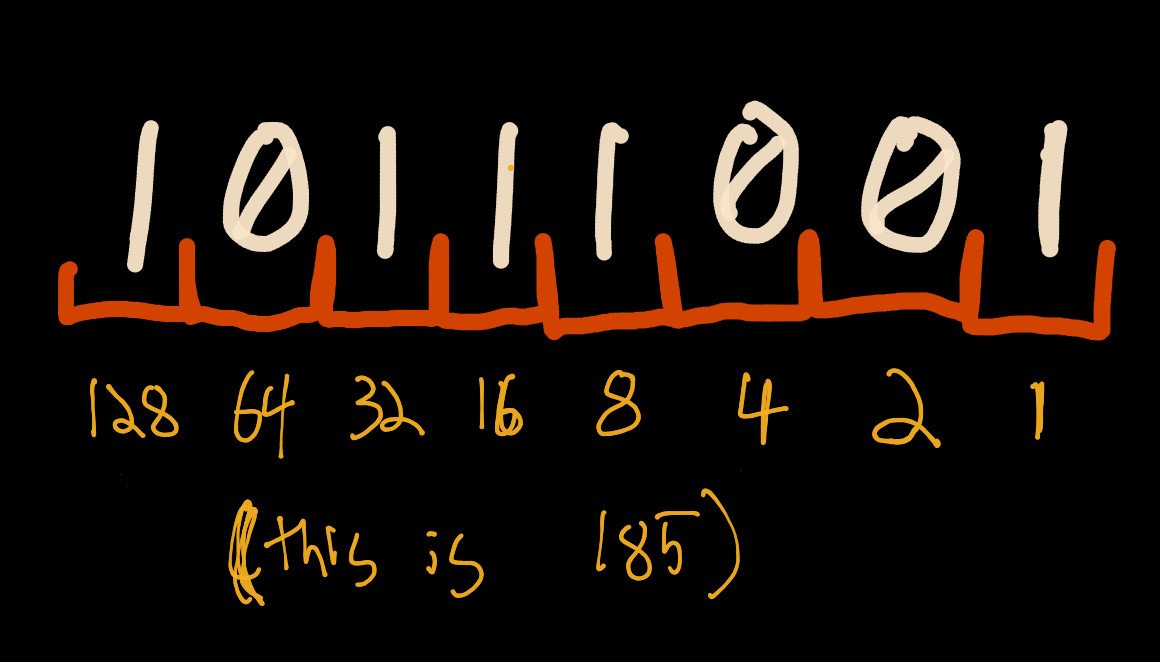Coin flips and most significant bits.

This week is just a few random thoughts I've had on coin flips and binary numbers.

If you flip a fair coin, there is a fifty percent chance of getting heads. If you pick a random number from 0 to 255, there is a fifty percent chance that the number will be greater than 127. While it might be obvious that we’re equally dividing the range of numbers in half and calculating the odds of being in one half or the other, it wasn’t until I took Applied Cryptography in the Spring of 2023 that it struck me: there is a beautiful simplicity in how this is represented in binary bits.

With binary numbers, there is something known as bit numbering. For the sake of simplicity, we’ll focus on a left-to-right representation of the most significant bit (the largest value in the binary number is on the left). By contrast, the right-hand side is the least significant bit (the smallest value in the number is on the right).

Now, let’s represent a coin in binary as either a 1 (heads) or a 0 (tails). This is a 1-bit number, either zero or one, so its most significant bit also happens to be its least significant bit.

In binary numbers, each digit is a doubling of the value next to it.

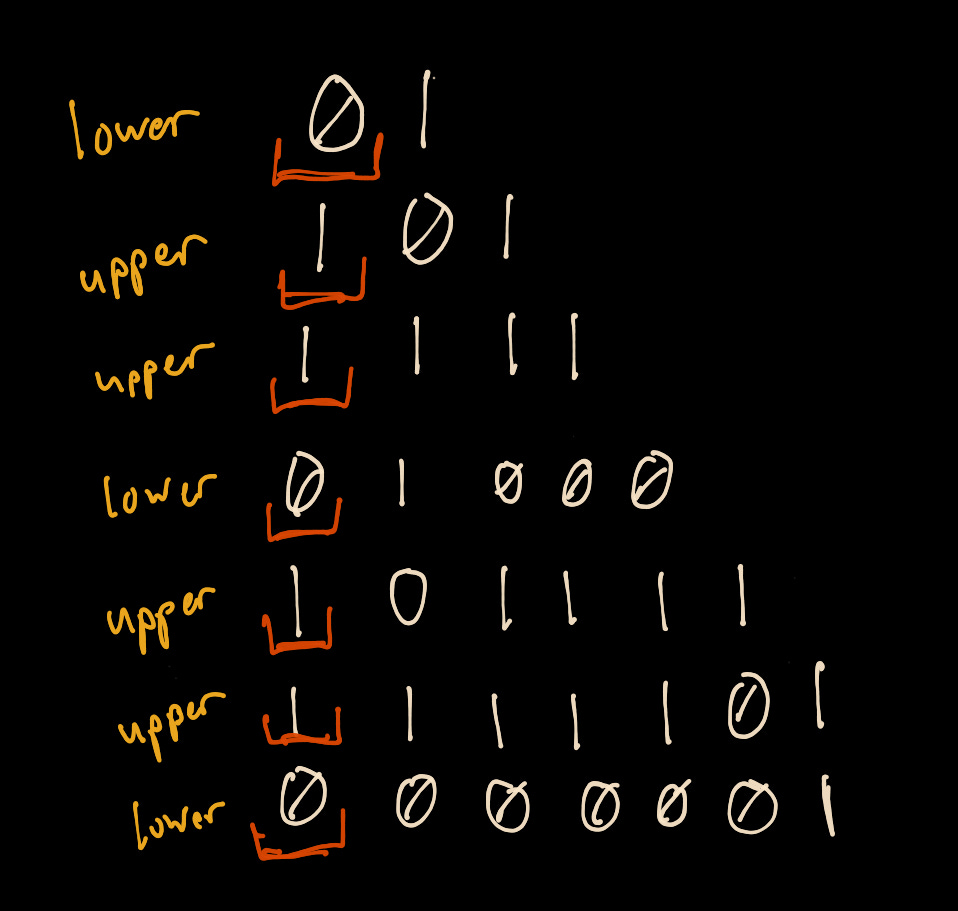
At a glance, even before calculating the value of the number, the most significant bit tells us whether or not it is in the upper half of the total possible numbers. If you think of this as a set of bits generated by a random number generator, it doesn’t matter what the value of any of the other bits might be; the most significant bit always dictates if it is a number in the “upper half” or “lower half” for the range of total possible numbers.

In fact, it doesn’t matter how large or small the number is; the most-significant bit represents the upper or lower half membership.

This means that we learn something important without knowing anything else about the number. If we see the value of the most significant bit, we know if the number exists in the upper or lower half of all possible numbers. It’s no different than a coin flip.

This week’s shareable links.

Not a ton of stuff this week because my wife, daughter, and I were too busy playing Legend of Zelda: Tears of the Kingdom. so ¯\_(ツ)_/¯ .

Real-Life Fractal Zoom by Henry Segerman

I’ve been a fan of Henry Segerman’s work for years. This video is no different. Who knew you could build fractals in the real world? There are lots of weird and fun little things in this video. And if you enjoy it, check out his other videos, like his work on Non-euclidean virtual reality or Braiding Gears.

Ditherpunk — The article I wish I had about monochrome image dithering

This blog post was excellent. It’s everything I never knew I needed to know about dithering. It’s well-written and beautifully designed.